للداله د حيث د ( س ) = س3 - 9 س2 +24 س - 4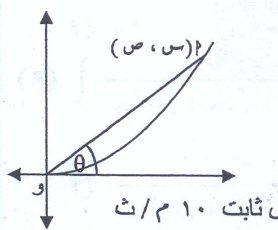
اولا : عين فترات التزايد والتناقض للداله د
ثانيا : اوجد القيم العظمى والصغرى المطلقة للدالة
فى الفترة [ -1 . 5 ]
ب ) يتحرك جسم ا ( س. ص )على المنحنة ص = س2
( كما فى الشكل المقابل ) بحيث يتزايد الاحداثى السينى له بمعدل ثابت 10م / ث
اولا : احسب معدل التزايد الاحداثى الصادى عندما س = 3 م
ثانيا : احسب معد لتزايد (0 ) زاوية ميل \vec{و\ ا} على محور السينات عندما س = 3 م